Задача 3.

     Побудуйте коло, що проходить через дві данні точки і дотикається до даної прямої.

     Аналіз. Нехай A і B – дані точки і L –дана пряма (мал. 7). Припустимо, що задачу розв'язано і шукане коло – k₁. Нехай точка B – центр інверсії. Коло k₂ – коло інверсії з радіусом BB₁, де точка B₁ – точка дотику до прямої L. Внаслідок інверсії пряма L перейде в коло k₃, яке проходить через точки B і B₁. Розглянемо шукане коло. Якщо коло проходить через центр інверсії, то воно переходить в пряму перпендикулярну лінії центрів. Коло k₁ проходить через точку A, тому інверсна пряма також повинна проходити через інверсну точку A₁. Якщо коло k₁ дотикалось до прямої L, то інверсна пряма також повинна мати точку дотику з колом k₃ інверсним прямій L. Точка дотику прямої з колом – точка C₁ – інверсна точці C, яка належить колу.

Мал.7

     Побудова. Будуємо данні точки A і B і пряму L. Будуємо коло k₂ – з центром в точці B і радіусом BB₁. Далі побудуємо фігуру інверсну прямій L, тобто коло k₃. Виконаємо перетворення інверсії точки A відносно центра інверсії B. Проведемо дотичну до кола k₃, яка проходить через точку A₁. Точка дотику – точка C₁. Побудуємо точку C інверсну точці C₁. Маємо три точки A,B і C, які належать шуканому колу. З'єднаємо їх і опишемо отриманий трикутник. Маємо шукане коло k₁.

Задача 4.

(Узагальнена задача Архімеда)

     У трактаті математика древньогрецького вченого Папа    (III ст.н.е.) міститься дві задачі розв'язані Архімедом.

1.   Візьмемо три півкола, що дотикаються одне одного і в одержану фігуру впишемо декілька кіл, що дотикаються одне одного і основних кіл. Нехай центри цих кіл O₁,O₂,O₃,O₄… Опустимо перпендикуляри із центрів O₁,O₂,O₃,O₄…, одержимо точки H₁,H₂,H₃,H₄… Потрібно показати, що O₁H₁=d₁, O₂H₂=2d₂, O₃H₃=3d₃, O₄H₄=4d₄… тобто відношення довжин перпендикулярів опущених із центрів кіл вписаних в арбелон до діаметрів цих кіл утворюють послідовність натуральних чисел.

2.   Дано два півкола, впишемо дотичні до цих півкіл кола з центрами O₁,O₂,O₃… Із центрів кіл проведемо перпендикуляри O₁H₁, O₂H₂, O₃H₃… O₁H₁=R₁, O₂H₂=3R₂, O₃H₃=5R₃… тобто відношення перпендикулярів до радіусів відповідних кіл дає послідовність непарних чисел.

     Античні вчені розв'язували ці геометричні задачі порівнюючи відрізки і, визначаючи відношення між ними. Для цього їм потрібно було складати довгі ланцюги пропорцій й рішення були дуже громіздкі.

     За допомогою перетворення інверсії можна одержати рішення задач Архімеда і навіть більш загального твердження: Нехай AB і AC діаметри півкіл. Впишемо в утворений рогоподібний кут послідовність кіл з радіусами R₁, R₂… що дотикаються одне одного. Розташування першого кола довільне. Позначимо через h_n довжину перпендикуляра опущеного із кола з радіусом r_n на AB, тоді відношення

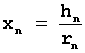
утворює арифметичну прогресію з різницею 2 (мал. 8).

Мал.8

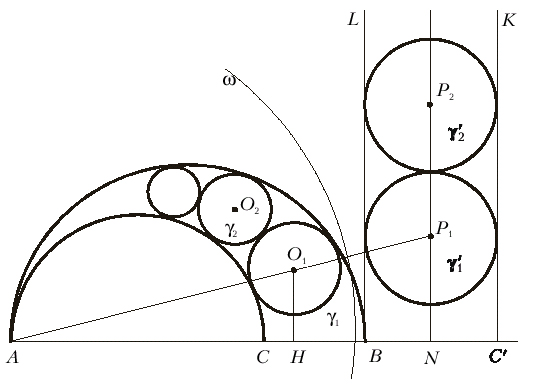
Доведення. Нехай O₁, O₂,… центри кіл g₁, g₂,… Будемо вважати     АВ = 2R, AC = 2r. Виконаємо інверсію отриманої конструкції відносно кола w довільного радіуса з центром в точці А. У результаті інверсії вихідні півкола перейдуть в промені BL і C’K, перпендикулярні прямій АВ, а g₁, g₂,…- в кола g’₁, g’₂,…, що дотикаються цих променів і по парно один одного. (Нагадаємо, що центри P₁, P₂,… цих кіл не є інверсними для точок O₁,    O₂,…) Позначимо через r радіуси отриманих кіл. Опустимо з центрів P₁ і P₂ перпендикуляри O₁H і P₁N на пряму АВ і позначимо O₁H = h₁ , P₁N = h. Кола g₁ і g’₁, як і трикутники AO₁H і AP₁N, гомотетичні з тим самим коефіцієнтом гомотетії. Тому

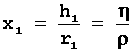
Для наступного кола маємо

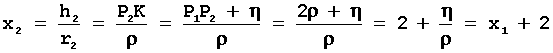
Аналогічно, для будь-якого натурального числа n маємо співвідношення

Отже, послідовність {x_n} являє собою арифметичну прогресію з різницею 2. Що й треба було довести.